Pythagoras Theorem
Created over 2000 years ago by the Greek mathematician Pythagoras, Pythagoras’ Theorem tells us how the three sides in a right-angled triangle are related. The ancient Greeks worked with lines and area rather that numbers and equations, so the theorem would have been expressed verbally and geometrically.
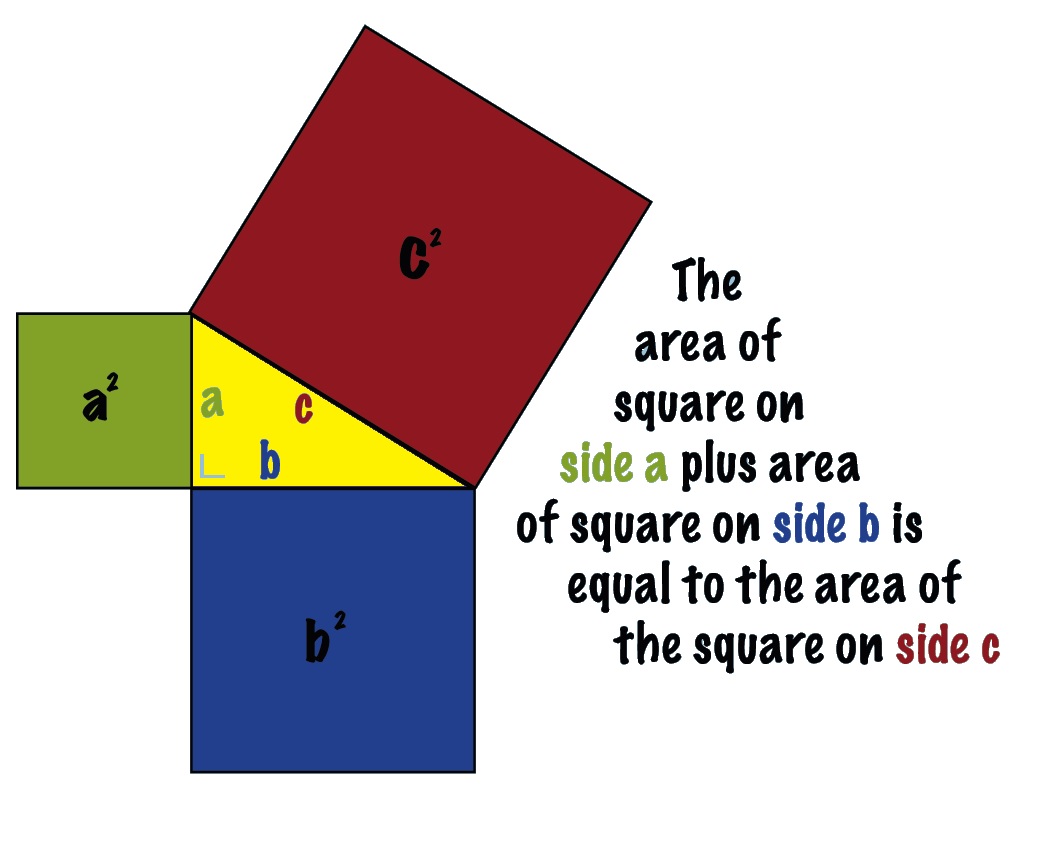
“The area of a square constructed using the longest side of a right angled triangle is the sum of the areas of the squares formed from the other two sides”.
Or more likely found in school maths books as
The square on the hypotenuse of a right angled triangle is equal to the sum of the squares on the other two sides.
Which is why a lot of adults might remember it as something to do with hippopotamuses
It wasn’t until more recent times that we arrived at the famous algebraic equation that every school student will be familiar with:
c² = a² + b²
Where c is the length of the hypotenuse (the longest side), a and b are the lengths of the other two sides, and the small raised 2 means ‘square’.
Pythagoras’ Theorem makes the connection between geometry and algebra, allowing us to calculate distance in terms of coordinates. It also inspired Trigonometry and so is a useful formula frequently used in architecture, navigation, surveying and in more recently is incorporated in the best current theories of space, time and gravity.

Pythagoras’ Mission
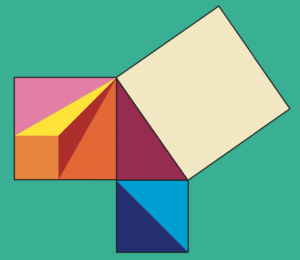
Pythagoras Theorem applies to all right-angled triangles. It tells us that if we build a square on each side of the triangles, the area of the square on the longest side of the triangle (hypotenuse) is equal to the areas of the other two squares added together. Try to test it using the colored pieces!
1) Try to cover the two smaller squares
2) With the same pieces try to cover the bigger square
TIP! You can ROTATE and also FLIP the pieces to solve the puzzle.
For further guidance here there is a template you can download.
CLICK HERE TO DOWNLOAD THE TEMPLATE
Due to the manufacturing process cuts may not be fully accurate.

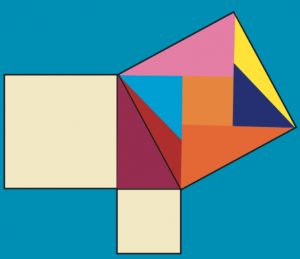
Pythagoras’ Mission – Solution