Answer: 4 children altogether
Mary has 2 brothers and one sister, while John has 2 sisters and 1 brother.
This sort of puzzle can be solved using a technique called simultaneous equations. This is a technique that is covered in Junior Certificate mathematics and is very powerful in finding unknown quantities in a system if one has enough information to piece together mathematically. It’s not really necessary for the above question that may be solved by in- formed “trial and error”, but we will take the opportunity of showing the technique here.
We have two related pieces of information:
1. Mary has twice as many brothers and sisters
2. John has twice as many brothers as sisters
We can express each of these with symbols and numbers. We use symbols as a shorthand code.
Here we will use the letter B to represent the number of boys and the letter G to represent the number of girls
1. “Mary has twice as many brothers and sisters” can be expressed symbolically.
The number of sisters Mary has is G-1. This is because Mary is a girl and therefore her number of sisters is the number of girls in the family minus one (herself). The number of brothers is the number of boys (B) and this is twice the number of sisters (2x(G-1)).
B =2(G-1), which multiplies out as
B = 2G – 2 (which we will call equation 1(eqn 1))
Likewise,
2. “John has twice as many sisters as brothers” can be expressed as
G = 2(B-1), which multiplies out as
G = 2B – 2 (which we will call equation 2(eqn 2))
Because both of these mathematical equations describe the same situation they can be combined.
If we take (eqn 1) B =2G-2 and insert this expression for B into (eqn 2) G = 2B-2, we get:
G = 2(2G-2) – 2
Which multiplies out as
G = 4G – 4 -2
Which is
G = 4G -6
If we subtract G from both sides
0 = 3G – 6
And if we add 6 to each side we get
3G = 6
And if 3G = 6 then G must equal 2.
Therefore the number of girls is 2.
Going back to equation 1:
B=2G-2
And putting in G=2
B = 2(2) – 2
B=4-2
B=2
So there are 2 boys and 2 girls in the family.

Answer: 20
This problem again relates to graph theory but this time the relations between each of the objects is different:
Pete will send four text messages: one to Sarah, one to Matt, one to Nina and one to Arturas.
Sarah, who has already received a text message from Pete, still needs to send four messages – one to each person.
This is the same for Matt, Nina and Arturas meaning that a total of 20 text messages will be sent.

Answer: 6
Displaying this puzzle in a square format allows for a visual solution and also an introduction to graph theory. This is the study of graphs where a graph is used to demonstrate relations between objects. In this case we are demonstrating the relations between four people.
We can see that Amy (in the red jumper) will have a total of 3 handshakes: one with Liam, one with Samira and one with Luke.
Liam has already shaken hands with Amy so he will have two more handshakes: one with Samira and one with Luke.
Samira will have already shaken hands with Amy and Liam so she will only have one more handshake with Luke.
Luke, at this stage, will have shaken hands with everyone in the group.
There will be a total of six handshakes for four people.

Answer: 30 games
This problem is more like the handshake problem and again introduces pupils to graph theory.
Let’s take Group D with the six teams of Republic of Ireland, Wales, Austria, Serbia, Moldova and Georgia.
Republic of Ireland will play ten games: two against Wales, two against Austria, two against Serbia, two against Moldova and two against Georgia.
Wales will have already played the Republic of Ireland twice so they will have eight games left to play: two against Austria, two against Serbia, two against Moldova and two against Georgia.
Austria will have already played the Republic of Ireland and Wales so they will have six games left to play against Serbia, Moldova and Georgia.
Serbia will have played against the Republic of Ireland, Wales and Austria so they will have four games left to play against Moldova and Georgia.
Moldova will have played every team twice at this stage apart from Georgia.
Georgia will then have played every team in the group twice.
There will be a total of 30 games for a group of six teams.
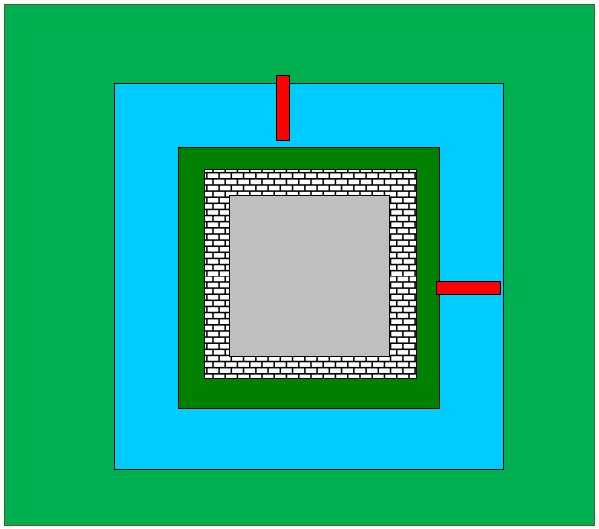

Calculations
 |
By Pythagoras the distance across at the corners can be calculated: 52 + 52 = 50 ?50m = 7.07m |
|---|---|
 |
Assuming a support overlap of 0.15m will be steady enough it is possible |

One way to solve this puzzle is by using equations. From the information given, we can write the following equations (initial’s are used to denote the child’s age):
- S = 3P (Sarah is 3 times as old as Max)
- M = 2P (Max is 2 times as old as Peter)
- L = M + 2 (Lucy’s age is equal to Max’s age plus 2 years)
- S + P + M + L = 26 (the sum of all 4 children’s ages is equal to 26)
Then we can substitute into Equation 4:
3P + P + 2P + 2P + 2 = 26
By standard algebraic rules,
8P +2 = 26
8P = 26 – 2 = 24
P = 24/8 = 3
We now know that Peter is 3 years old, and Max is twice Peter’s age (Equation 2), therefore Max is 6.
Now we can calculate Lucy’s age using Equation 3. If Lucy is 2 years older than Max, Lucy must be 8.
Answer: 8
Another method that could be used to solve this problem is bar modelling.