Pascal’s Triangle:

We present some activities below:

• DIY Maths Project: Make a Galton board-Pascal’s triangle
• Probability Questions.
• Combination Questions.
• Pattern Activity.
• Serpinski’s Triangle Activity.
• Fibonacci Rabbit Question.
• Fibonacci Sequence Activity.

 

Historical Background:

Blaise Pascal was a French physicist, inventor, mathematician and philosopher. He is most famous for studying the properties of fluids, probability theory and projective geometry. Blaise pascal was born in Clermont, France in 1623-1662.

His father, Étienne Pascal decided to teach Pascal himself. He also decided Blaise was not to study mathematics before the age of 15 and removed all mathematics texts from their house. However, curiosity risen in Blaise and when he was 12 years old, he started to work on geometry. His first discovery was that the sum of three angles in a triangle equals two right-angled triangles. Blaise’s father eventually changed his mind and allowed him a copy of Euclid.

Blais began accompanying his father to Mersenne’s meetings at 14 years old. Mersenne was an ordained catholic priest and a French mathematician. He was known as the “academy” of polymath. Blaise presented one piece of paper containing several projective geometry theorems to one of Mersenne’s meetings at 16 years old. One of Blaise’s most famous theorems from algebraic geometry known as the “mystic hexagon” was presented. Pascal’s Theorem or the Hexagrammum Mysticum Theorem states that six points lie on a conic if and only if three points generated by the original six lie on a line.

In 1639, Blaise’s father was appointed a tax collector for Upper Normandy. Pascal invented the “pascaline”, one of the first digital calculators with movable dials to help his father Étienne with collecting taxes. His work on the digital calculator lasted for three years. He built 20 calculating machines in his time.

In 1648, Blaise observed that the pressure of the atmosphere decreases with height and deduced that a vacuum existed above the atmosphere.

From May 1653 Pascal worked on mathematics and physics writing Treatise on the Equilibrium of Liquids (1653) in which he explains Pascal’s law of pressure.

In 450BC, the indian mathematician Pingala first discovered Pascals triangle and named it the “Staircase of Mount Meru” after a sacred Hindu Mountain. In the early 11^th century, the Persian poet and mathematician Omar Khayyam called it the “Khayyam triangle”.Then, in the 13^th century, chinese mathematician Jia Xian also discovered the triangle and named it after his successor “Yang Hui’s triangle”.

At first, the triangle looks complex but within Pascal’s triangle there are incredible mathematical patterns hidden within. Pascal was one of the first European mathematicians to investigate the mathematical patterns and properties of the triangle

Left image is the staircase of mount meru(india).

Middle image is the Khayyam triangle (Iran).

Right image is Yang Hui’s triangle (China).

The first modern form of public transport in the world

One of Blaise Pascal’s last achievements was the first modern form of public transport known was the carrosses à cinq sols. Paris was the fifth largest city in the world at that time and needed a successful cheaper and more accessible transport system to aid the population. The idea was a horse-powered bus service with a set amount of carriages to drive through Paris on set routes and would stop at set places along the route. Thus the world’s, first public transportation system in action took place on March 18 in 1662. According to Marc Gaillard, the carrosses ran until 1677.

Pascal and Physics:

Pascal was fascinated by the concept of the vacuum, and he conducted important research. In 1647, Pascal proved that a vacuum does exist above the atmosphere. He also found out that atmospheric pressure can be measured by using real weights. In 1647, he discovered what is now known as Pascal’s law or Pascal’s principle. It states that pressure applied to a confined liquid is transmitted undiminished through the liquid in all directions regardless of the area to which the pressure is applied. Pascal’s law is the underlying principle of hydraulic press, used in many devices such as hydraulic brakes in vehicles. Applying Pascal’s principle, he also used it to invent the syringe.

Famous Quotes from Blaise Pascal:

• Truth is so obscure in these times, and falsehood so established, that, unless we love the truth, we cannot know it.
• We sail within a vast sphere, ever drifting in uncertainty, driven from end to end.
• We view things not only from different sides but with different eyes; we have no wish to find them alike.
• In faith, there is enough light for those who want to believe and enough shadows to blind those who don’t.
• Nature is an infinite sphere of which the centre is everywhere and the circumference nowhere.

 

 

Probability:

Professional Parisian gambler, Antoine Gombaud turned to Pascal to determine the fairest way to distribute the pot and questions regarding gambling. He realized that events don’t happen randomly. Pascal’s interest in games of chance started and this led him to collaborate with Pierre de Fermat and establish the fundamental laws of probability. Both mathematicians founded a new branch of mathematics: the theory of probabilities, which is now used in numerous fields in the world e.g., climatic models to predict stock market fluctuations.

Blaise Pascal developed a mathematical theory of probability, based on his interest in gambling. He also carried out important work into the relationship between gases and liquids.

Activities

Probability:

Professional Parisian gambler, Antoine Gombaud turned to Pascal to determine the fairest way to distribute the pot and questions regarding gambling. He realized that events don’t happen randomly. Pascal’s interest in games of chance started and this led him to collaborate with Pierre de Fermat and establish the fundamental laws of probability. Both mathematicians founded a new branch of mathematics: the theory of probabilities, which is now used in numerous fields in the world e.g., climatic models to predict stock market fluctuations.

Blaise Pascal developed a mathematical theory of probability, based on his interest in gambling. He also carried out important work into the relationship between gases and liquids.

Pascal’s Triangle and Normal Distribution Curve

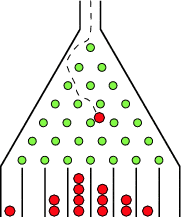
An amazing little machine created by Sir Francis Galton is a Pascal’s Triangle made out of pegs. It is called The Quincunx or “Galton Board”

Balls are dropped onto the first top peg and then bounce down to the bottom of the triangle where they collect in little bins.

Each time a ball hits one of the pegs, it bounces either left or right.

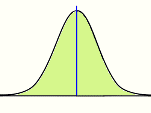
But this is interesting: if there is an equal chance of bouncing left or right, then the pegs collecting in the bins form the classic “bell-shaped” curve of the normal distribution.

You can look at Pascal’s Triangle. In fact, the Quincunx is just like Pascal’s Triangle, with pegs instead of numbers. The number on each peg shows you how many different paths can be taken to get to that peg. Amazing but true.

DIY Maths Project: Make a Galton board-Pascal’s triangle

Here is a nice activity from Abakus.com 

Materials:

1. Printable
2. Cork board (6″ x 11″, 1/2″ thick)
3. White glue
4. Pins
5. Popsicle sticks (11)
6. Straw
7. Scissors
8. Foam tape
9. Round beads – 1/4″

Printable:

http://images.kiwicrate.com/diy_ad/KiwiCo-Mesmerizing-Mathematics.pdf

Steps:

1. Gather all materials.
2. Glue the printable to one side of the corkboard. Then, trim the paper to the corkboard.
3. Push a pin into every dot.(You may need an adult to assist you).
4. Glue a popsicle stick on top of every line, using beads to help evenly space the popsicle sticks. Let them dry for at least ½ hour.
5. Cut 2 inches of the straw and glue it along the top of the corkboard centered above the first row of pins. Lean the corkboard up against a wall and drop some beads down the straw. The more beads you drop, the better!

Task: Observe the distribution of the beads.

Question: Can you see any patterns?

Human Galton Board Activity:

https://blogs.adelaide.edu.au/maths-learning/2018/07/09/the-human-galton-board/

Probability Questions using Pascal’s Triangle:

How to count the rows in Pascals triangle:

 

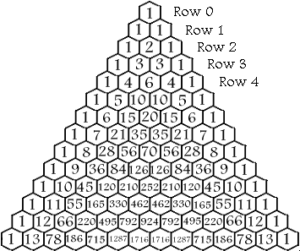
A coin is tossed two times. Find the probability of getting 2 tails?

The combinations are: HH,TH,HT,TT.

There is 1 combination that gives two heads.

There is 2 combinations that gives one head and one tail.

There is 1 combination that gives two tails.

The combination gives this order:  1, 2 ,1.

Does this look familiar?

It’s the 2^nd row of Pascals Triangle.

The probability of getting 2 tails is 1 combination out of 4 total combinations.

¼= 0.25 or 25%.

Rule: The numbers in each row of pascal’s triangle correspond with the number of combinations for getting heads and tails in a coin toss.

 

E.g. Tossing a coin 3 times, look at the 3^rd row to find the number of combinations for heads and tails.

The combination is 1, 3, 3, 1.

The 1 represents the combination that gives exactly 3 heads.

The 3 represents the combination that gives 2 heads, 1 tail.

The next 3 represents the combination that gives 1 head, 2 tails.

The final 1 represents the combination that gives 0 heads, 3 tails.

Question: A coin is tossed five times. Find the probability of getting exactly 2 tails?

Additional Question: A coin is tossed ten times. Find the probability of getting 5 heads and 5 tails?

Note: Remember to get the probability you must divide the number of favourable events by the number of total events.

  

Combination Questions using Pascal’s Triangle:

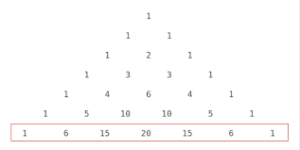
To determine how many combinations of an object are possible, you can use the formula for nCr and Pascal’s triangle.

The “n” corresponds to the row in the triangle.

The “r” corresponds to the column in the triangle.

This represents your number of combinations.

For example, you have 6 family members, and you want to take 4 of them on holiday. How many different ways could you pick the 4 family members?

6 is the total and represents “n”.

4 is the number of people we can take at a time and represents “r”.

Thus, countdown to row 6 and to column 4.

Note: Do not count the outer number “1” as a column”.

There are 15 different combinations of family members we can take on holidays.

OR

Using nCr:

6C4=6! / 4!4! = 15

Question: You have 20 rugby players, and you must pick 15 of them to play in a rugby match. How many different ways could you pick 15 players for the match?

Additional Question: Following the above question. However, the rugby captain must be picked. How many different ways could you pick the players for the match?

More Math’s activities to investigate Pascal’s Triangle:

Pattern Activity:

Task 1 Completing Pascal’s Triangle:

Start with a 1 at the top.

Each number below is the sum of the two numbers above it.

The outside numbers are always 1.

Can you fill the triangle?

Task 2 Mod-2 Colouring:

Colour all the entries divisible by 2 black.

What do we get?

This is called the “Mod-2″ colouring.

Task 3 Mod-3 Colouring:

Colour all the entries divisible by 3 black.

What do we get?

Task 4 Experiment:

Time to experiment.

Now, choose another number and see if there is a cool pattern.

Some examples attached below:

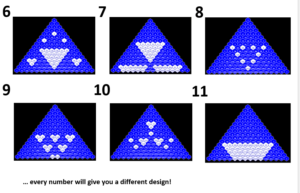
Task- Sierpinski Triangle:

Shade in all the even numbers in pascal’s triangle.

This is called the Sierpinski triangle.

You can do a big project connecting everyone’s triangle in the classroom.

Shapes like the Sierpinski Triangle are known as fractals. Fractals are characterized by a basic pattern that can endlessly repeat, whilst getting smaller in size each time. The triangles are just building blocks.

Activity on the Fibonacci sequence:

Looking at Pascal’s Triangle diagonally.

From the top section, add the numbers along the same diagonal row together.

Do you recognize this pattern of numbers?

This pattern of numbers is the Fibonacci Sequence!

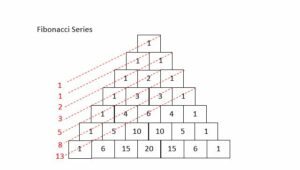
Fibonacci Sequence:

The sum of the numbers diagonally gives you the Fibonacci numbers.

It is useful when doing sequences and series!

The Fibonacci Sequence is the series of numbers: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

The next number is found by adding up the two numbers before it.

Questions: Do you see a sequence in the fibonacci sequence relating to odds and evens?

Odd fact: The sequence goes even, odd, odd, even, odd, odd, even, odd, odd,

Question: What is the following number after 377 in the fibonacci sequence?